Euclidean Geometry

The following section presupposes Set Theory, Topology and Nonstandard Analysis.

Definition: Let \(R\) a Euclidean space as subspace of \(\mathbb{R}^{n}\) with \(n \in {}^{\omega }\mathbb{N}_{\ge 3}\) (see Set Theory). Two distinct points as elements of \(R\) are called pair (of points). A one-dimensional point set in \(R\) is called a line if each point has at least one and at most two gaplessly neighbouring points. A one-dimensional subspace of \(R\) is called straight line, a two-dimensional one is said to be a plane. The distance is given by the Euclidean norm \(||\cdot||\) and results summed up in the Euclidean arc length \(A.\triangle\)

Definition: A line segment is a connected subset of a straight line, whose starting point and end point determine it precisely and have to only one neighbour finite distance. Two line segments are said to intersect if they have one interior point in common. Two line segments are said to be parallel if one line may be obtained from the other by means of a translation. All points of a plane with the same distance (called radius) to another point constitute a circle, which forms with its interior a disk.\(\triangle\)

Result: By defining short straight lines, many counterexamples can be given based on the above to Pasch’s axiom, the axiom of line completeness, as well as various other axioms and their equivalents. The subspace concept can prove Hilbert’s incidence axioms I.6 and I.8. If a straight line uniquely defines a parallel straight line running through a given point by their shortest distance, the parallel postulate is dispensable in Euclidean Geometry. The axioms of order and congruence are redundant.

Contrary to Hilbert’s incidence axiom I.4, three distinct points are not enough to uniquely determine a plane since there are different infinities. Hilbert’s incidence axiom I.7 is false¹vgl. Hilbert, David: Grundlagen der Geometrie; 2. Aufl.; 1903; Teubner; Leipzig; p. 2 – 17, since planes are yet limited in infinity and can precisely intersect in one point. All (three ancient) exactly unsolvable problems may be solved with arbitrary precision by the fundamental theorem of set theory via the intercept theorem and Farey sequences²Scheid, Harald: Zahlentheorie; 1. Aufl.; 1991; Bibliographisches Institut; Mannheim, p. 62 f..

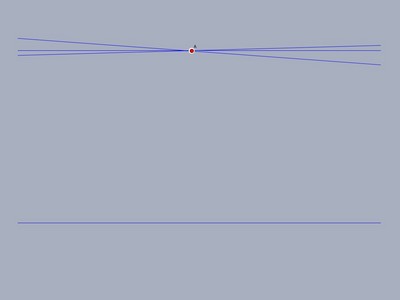
Rating two straight lines only as parallel when they lie in the same plane and do not intersect, the parallel postulate does not hold: The reciprocal of the distance between the straight line and the given point may be greater than infinity or smaller than \(|{}^{\omega }\mathbb{N}|\), and then infinitely many distinct straight lines can be found that pass through the given point without intersecting the original straight line. Formulating the axiom of completeness vaguely, Hilbert renders it finally unapt in future.

The Archimedean axiom must be extended to the case where a segment is marked off an infinite natural number of times without exceeding the starting point or end point of a straight line. It must be in the finite case replaced by the Archimedean theorem (see Set Theory). Pasch’s axiom is also unnecessary, since every straight line must be fully contained in the interior of some triangle due to its maximum length, and hence so must its boundary, provided that one of its points is in this interior.

Normal theorem: For \(n \in {}^{\omega }\mathbb{N}_{\ge 2}\), every convex set \(S\) from \({}^{\omega }\mathbb{R}^{n}\) contains a point lying on \(\hat{n}\) distinct normals through \(\partial S\) (also through a vertex), since this is possible every \(90°\) in the plane³cf. Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K.: Unsolved Problems in Geometry; Reprint of 1st Ed.; 2013; Springer; New York; p. 14 f..\(\square\)

Toeplitz’ conjecture: Every Jordan curve admits an inscribed square.

Counterexamples: The right-angled triangle with two sides of length \(\iota\) and the obtuse triangle where a vertex of at most one inscribed square is infinitesimally moved within the limits.\(\square\)

Theorem: Infinitesimally juxtaposing equichordal points within the limits leads to a Jordan domain with more than one equichordal point⁴cf. loc. cit. p. 9 f..\(\square\)

Fickett’s theorem: Any relative position of two overlapping congruent rectangular \(n\)-prisms \(P\) and \(Q\)⁵loc. cit. p. 25. with \(n \in {}^{\omega }\mathbb{N}_{\ge 2}\) and \(\grave{m} := \hat{n}\) implies for the exact standard measure \(\mu\), which is \(A\) for \(n = 2\):\[\widetilde{m} < r := \mu(\partial P \cap Q)/\mu(\partial Q \cap P) < m.\]Proof: The underlying extremal problem has its maximum for rectangles with side lengths \(s\) and \(s + \hat{\iota}\). Putting \(q := 3 – \hat{\iota}\tilde{s}\) implies min \(r = \tilde{q} \le r \le\) max \(r = q\). The proof for \(n > 2\) works analogously.\(\square\)

© 2010-2017 by Boris Haase

top