The following Julia programme implements the so-called FastShift algorithm for fast matrix multiplication of integer matrices using bit operations and recursive subdivision. Comments in the source code explain important parts of the implementation.
# 🔠 FastShift Algorithm in Julia, Authors: Boris Haase & Math AI 🧠 from April 17, 2025
using LinearAlgebra, BenchmarkTools, Printf, Random, Base.Threads
const D = 256 # Ceiling value, less than or equal to G
const E = 8 # Exponent roughly greater than five
const R = 64 # Threshold for switching to multithreading
const G = 1 << E # Desired upper bit limit
const I = BigInt(1) # One as a BigInt
const L = (I << D) - I # Upper/lower limit for random values
const T = AbstractMatrix{BigInt} # Matrix type for large integers
const S = G << 1 # Shift factor as a power of two
const O = BigInt(0) # Zero as a BigInt
# 🔧 Helper functions for modular division and matrix multiplication
remR(x, t, u, v) = x < O ? -adjR(-x & u, t, v) : adjR(x & u, t, v)
adjR(x, t, v) = x < v ? x : x - t
divR(x, v, s) = (x + v) >> s
function simd_mul(A::T, B::T, n::Int)::T # Conventional SIMD matrix multiplication
C = zeros(BigInt, n, n)
@inbounds for i in 1:n # No bounds checking for indices
for j in 1:n
z = O
@simd ivdep for k in 1:n # No interdependencies in this loop
z += A[i, k] * B[k, j]
end
C[i, j] = z
end
end
return C # Return the matrix product
end
# 🔡 FastShift recursive multiplication for matrices of large integers
function fastshift(A::T, B::T, n::Int, s::Int)::T
n <= R && return simd_mul(A, B, n) # Use standard multiplication for small n
m = n >> 1 # Split matrices into four blocks
M = 1:m # Left index of the matrix
N = m+1:n # Right index of the matrix
v = I << (s - 1) # Reference value for nearest neighbour
t = I << s # Modulus for division with remainder
r = s << 1 # Next recursion depth
u = t - I # Bitmask to extract the lower half
R1 = (B[M, M] .<< s) .+ B[M, N] # Top row of combined matrix
R2 = (B[N, M] .<< s) .+ B[N, N] # Bottom row of combined matrix
if n > R # Use threads for large matrices
t1 = @spawn fastshift(A[M, M], R1, m, r)
t2 = @spawn fastshift(A[M, N], R2, m, r)
t3 = @spawn fastshift(A[N, M], R1, m, r)
S4 = fastshift(A[N, N], R2, m, r) # Matrix on main thread
S1 = fetch(t1) # Retrieve results from other threads
S2 = fetch(t2)
S3 = fetch(t3)
else
S1 = fastshift(A[M, M], R1, m, r) # No threading for small matrices
S2 = fastshift(A[M, N], R2, m, r)
S3 = fastshift(A[N, M], R1, m, r)
S4 = fastshift(A[N, N], R2, m, r)
end
C1 = divR.(S1, v, s ) .+ divR.(S2, v, s ) # Modular division as defined
C2 = remR.(S1, t, u, v) .+ remR.(S2, t, u, v)
C3 = divR.(S3, v, s ) .+ divR.(S4, v, s )
C4 = remR.(S3, t, u, v) .+ remR.(S4, t, u, v)
return [C1 C2; C3 C4] # Return the full matrix product
end
# 🕔 Benchmark for C = A * B with correctness check against Julia's standard implementation
function main()
@assert D <= G "Ceiling value must not exceed bit limit G"
println("⏱️ Benchmark for the FastShift algorithm – m from 1 to 10")
println("═════════════════════════════════════════════════════════")
println("🕸 Threads: $(nthreads())") # Expected to run with four threads
for m in 1:10
n = 1 << m # Dimension as a power of two
A = rand(-L:L, n, n) # Left random matrix with large integers
B = rand(-L:L, n, n) # Right random matrix with large integers
println("\n❓ Test: 2^$m × 2^$m → $n × $n") # Display test info
t_fasts = @elapsed C_fasts = fastshift(A, B, n, S + m)
@printf("🔢 Runtime for FastShift: %10.4f seconds\n", t_fasts)
t_julia = @elapsed C_julia = A * B # Measure Julia's standard multiplication
@printf("❕ Runtime for Julia A*B: %10.4f seconds\n", t_julia)
println("💯 Equality of results:") # Check if results match
println(C_fasts == C_julia ? "✅ FastShift ≙ Julia" : "❌ FastShift ≠ Julia")
end
end
# ▶️ Start execution
main()
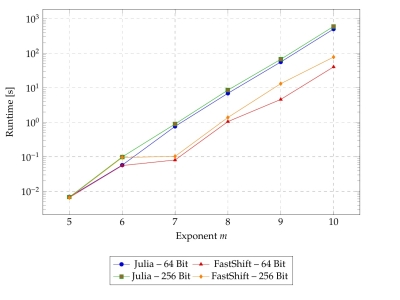
| \(m\) | \(T_j^{64}\) | \(T_f^{64}\) | \(T_j^{64}\)/\(T_f^{64}\) | \(T_j^{256}\) | \(T_f^{256}\) | \(T_j^{256}/T_f^{256}\) |
|---|---|---|---|---|---|---|
| 5 | 0.0069 | 0.0066 | 1.0455 | 0.0068 | 0.0065 | 1.0462 |
| 6 | 0.0573 | 0.0557 | 1.0287 | 0.0988 | 0.0951 | 1.0389 |
| 7 | 0.7557 | 0.0805 | 9.3882 | 0.8866 | 0.1026 | 8.6414 |
| 8 | 6.8593 | 1.0416 | 6.5865 | 8.4964 | 1.3699 | 6.2029 |
| 9 | 55.2878 | 4.5610 | 12.1228 | 66.0994 | 13.0518 | 5.0654 |
| 10 | 496.9587 | 39.9252 | 12.4443 | 592.4100 | 76.8205 | 7.7094 |
Modeling the Runtime Behaviour
The runtime can be further reduced by using suitable pointer arithmetic. The nonlinear function \(T_n \sim n^a\) modeled with Mathematica and compared with both \(T_n \sim n^{\hat{a}}\) and \(T_n \sim n^{\hat{a}} + b\) yields the following results for 64 bit: \(T_j^{64} = \mathcal{O}(n^{2.32})\) and \(T_f^{64} = \mathcal{O}(n^{1.96})\). Analogously, 256 bit yields: \(T_j^{256} = \mathcal{O}(n^{2.35})\) and \(T_f^{256} = \mathcal{O}(n^{2.05})\).
© 2025 by Boris Haase